简介
或许你是第一次接触寻路算法,发现网上资料虽然不少,但你更想直观看到寻路算法工作时的样子;或许你已经写过许多寻路算法,但却不知道如何美观方便地可视化出来,那么,这套可以在浏览器上运行的寻路算法可视化程序绝对值得你一看。

这是一款可以在浏览器上运行的程序。
程序作者:qiao
程序下载:https://github.com/qiao/PathFinding.js
在线演示:PathFinding.js
如果无法访问 github,也可在网盘下载我汉化过的版本:
链接:https://pan.baidu.com/s/1pELMWLvXipYz9G43PPhjFA 提取码: 1ecz
解压后打开文件夹 -> visual -> index.html 就可以在本地浏览。如果无法正常显示,请更换 chrome 或 firefox 等现代浏览器。
这套程序包含的五种算法的资料很多,就不再赘述了。比较好玩的是不同的距离计算方式。
曼哈顿距离
Manhattan distance。如果游戏使用的是矩形网格地图,而在网格之间只能上下左右移动,那么就可以使用曼哈顿距离。据说这套算法是专门为出租车司机设计的,因为汽车只能沿着划分好的街道前进,而不能任意斜着穿过楼房。
假设第一个点的 x 坐标是 x1,y 坐标是 y1,第二个点的 x 坐标是 x2,y 坐标是 y2。
那么这两个点的曼哈顿距离就是 |x1 - x2| + |y1 - y2|,即两点横纵坐标差之和。
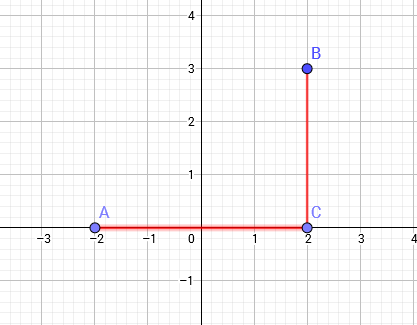
比如 AB 两点的曼哈顿距离就是 |2 - (-2)| + |3 - 0| = 7。
在 A 星算法中,我们也可以将结果再乘上 D。D 是花费参数,即从一个网格到另一个网格的花费。一般只需将其设置为 1 就行了。但也可以增加 D,这意味着放弃了最优路径,而追求更快的算法效果。相反,调低 D 意味着让算法更慢而最终路径更短。

例如,下面这张图是将权重即 D 调整为 10 的结果,路径长度 34,时间 0.8ms。
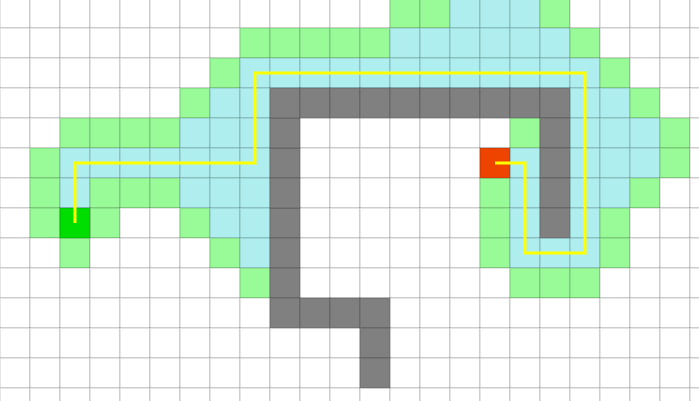
而下面这张图是将权重即 D 调整为 1,路径长度 28,时间 1.3ms
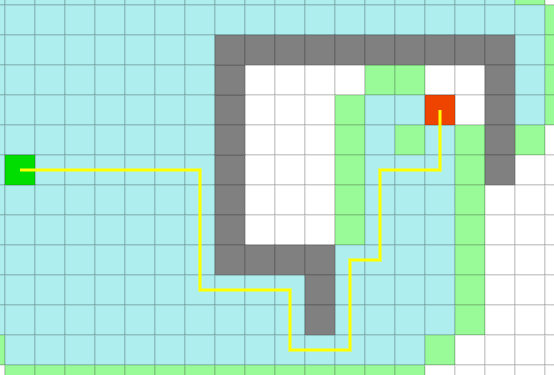
对角距离
Diagonal distance。在之前说到的地图中,如果允许沿对角线移动,即上下左右,左上,左下,右上,右下八个方向移动,那么就需要使用对角距离。
使用的算法如下,其中 D 是沿着上下左右四个方向移动一个网格的花费,而 D2是沿着左上,左下,右上,右下这四个对角线方向移动一个网格的花费。
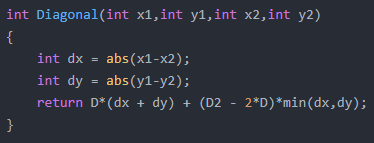
同样,如果将 D 设置为 1,而 D2 设置 1,那么这就叫做切比雪夫距离(Chebyshev distance)。
上述两点的切比雪夫距离为 |x1 - x2| 和 |y1 - y2| 中的最大值,即即两点横纵坐标差的最大值。
比如 A (2, 3) 和 B (-2, 0) 两点,切比雪夫距离就是 |2 - (-2)| 和 |3 - 0| 中的最大值即 4。
同样,如果将 D 设置为 1,而 D2 设置为根号 2,那么这就叫做 octile 距离。
欧几里得距离
如果地图不再被划分成网格,玩家可以在任意位置向任意方向移动的话,就可以用欧几里得距离了。
欧几里得距离就是我们从小用到大的经典距离计算公式,即
sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1))
或是这样写:
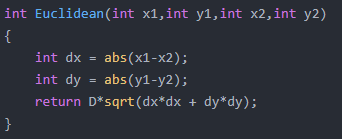
sqrt 用于开平方根。欧几里得距离一般要比曼哈顿距离短,但由于开平方根需要消耗一些计算资源,所以算法实际执行起来要慢一些。
于是有些人推荐去掉这个开平方根的步骤,直接把 ((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)) 作为结果返回。
但在 A 星算法 f = g + h 中,如果距离很长,距离函数 h 将变得很大,这时候估算函数 g 将几乎不起作用。这时候 A 星算法就退化成了最佳优先搜索算法。
也许可以通过把 D 设置得很小来让 h 不要那么大,但这时候如果距离很短,那么距离函数 h 将变得更小,与估算函数 g 相比几乎不起作用。这时候 A 星算法就退化成了 Dijkstra 算法。
如果开平方根消耗的资源仍然非常显著,那么我们可以用快速近似开平方根算法来代替一般的开平方根算法,或者干脆用 octile 距离来近似代替欧几里得距离。
节点距离
下图将在每个网格上都设置了节点,并连接起来。
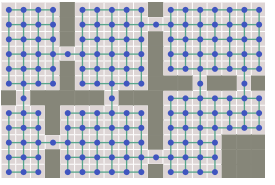
但有时候,并不需要那么复杂,于是干脆将这些网格点都去掉,改为设置好的节点,加上规划好的路径。也就是只保留部分网格点。从一个路点到另一个路点,下面左图允许使用最短直线距离,而下图右只允许沿着网格。而探讨如何在这些不规则路径上移动的领域,叫做图论。




没想到在论坛上也能看到这个= =
这个寻路是只考虑两个轴向么,是否能沿用到三维坐标系空间X.Y.Z中呢
@charon张:3d用navmesh寻路